New Scientist Enigma 152: The highways of Genoland revisited

Following my post on The highways of Genoland, Jim Randell pointed out that the original puzzle had missed a round trip, and that there are actually four round trips. The missing round trip uses highways 1,2,3,4,D (not necessarily in that order).

I wondered what a solution would look like if the fourth round trip had been included in the original puzzle:

As before, no pair of cities is connected by both a national and provincial highway. There are two possible configurations of connections that have eight connectors connecting five nodes:

Configuration A does not provide four round trips, so the five cities are connected in configuration B. We can immediately deduce which city is Geno:

The four  round trips 1,3,4,B,C;   1,2,A,C,D;   2,3,A,B,C;   1,2,3,4,D are in some order: 

Highways 1,2,3,C appear in three round trips (green). 4,A,B,D appear in two round trips (orange)

Geno is reached by the highways that appear in two round trips, namely 4,A,B,D

New Scientist Enigma 152: The highways of Genoland

This was a particularly tricky puzzle to solve with a computer algorithm, as demonstrated by Jim Randell's solution, so here is a manual solution.

The problem statement is:

The five cities of Genoland are interconnected by four national highways A, B, C and D. They are also independently linked by four provincial highways 1, 2, 3 and 4. Each highway connects two cities and Geno is the only city which can be directly reached from every other city. A round trip of the five cities involves the five highways 1, 3, 4, B and C or 1, 2, A, C and D or 2, 3, A, B and C (not necessarily in the order given).

Which of the highways reach Geno?

No pair of cities is connected by both a national and provincial highway (this can be deduced from the round trips). There are two possible configurations that have eight highways connecting five cities:

Configuration A does not provide three round trips, so the five cities are connected in configuration B. We can immediately deduce which city is Geno:

The three round trips are:  

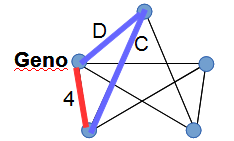
Highway C appears in all three round trips, so we can deduce which highway is C. Highways D and 4 appear in only one round trip each, so we can also deduce 4 and D (national highways are blue, provincial are red)

Highway 1 is in the same round trips as highways 4 and D, so we can deduce highway 1:

As all cities are connected via provincial highways, the remaining highway from the top city must be a provincial. Similarly, as all cities are connected via national highways the remaining highway connecting the bottom right city must be a national:

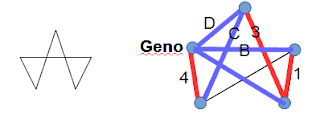
The round trip using highway 4 uses highways 1,3,4,B,C, so we can deduce which highways are B and 3 :

Similarly, the round trip using highway D uses highways 1,2,A,C,D so we can deduce which highways are A and 2 :

So Geno is reached by highways A,B,D,4

Hamiltonian Cycles on a Square Grid, part 2

The algorithm in my first post on this topic used some of the ideas in  R. Stoyan and V. Strehl: Enumeration of Hamiltonian Circuits in Rectangular Grids. Journal of Combinatorial Mathematics and Combin.Computing 21 (1996), 197-127, but did not employ the construction technique suggested in their paper.

Here is a modified algorithm, with vastly improved performance, using most of the construction method suggested by Stoyan and Strehl.

The algorithm constructs all 1,072 Hamiltonian cycles on a 6 by 6 grid in about 100ms, and all 4,638,576 Hamiltonian cycles on an 8 by 8 grid in about 20 minutes. 

Here, the algorithm runs out of steam, as a 10 by 10 grid has 467,260,456,608 cycles (Sloane A003763)



To construct N by N Hamiltonian cycles, the algorithm builds up  "induced subgraphs" (see diagram at left) of an (N-1) by (N-1) square graph one cell at a time, starting with the top row and working across each row in turn.










The top row is constructed by observing that the corner cells have to be inside the Hamiltonian Cycle, and that no two outside cells can be adjacent.

From then on, cells are added by testing whether a cell can be inside or outside (or both or neither) according to the rule that no 2 by 2 block can be any of these patterns:

A 2 by 2 block $a,b,c,d$ will match one of the four patterns iff $a=d$ and $b=c$




Additional tests check that:

• no 2 adjacent cells on the perimeter can be outside
• the total number of inside and outside cells does not exceed   $\frac{N^2-2}{2}$ and $\frac{(N-2)^2}{2}$ respectively
• After the completion of a row, all inside cells are connected to the row just completed.

Python implementation

Here is the Python code for the algorithm. 

Hamiltonians(N) yields all the Hamiltonian cycles for an N by N grid.

Constructing Hamiltonian Cycles on a Square Grid

Background

A solution to New Scientist Enigma puzzle 1431 led me to consider how to generate all Hamiltonian Cycles for an N by N square grid.

The obvious way to generate Hamiltonian cycles for any graph is to find all Hamiltonian paths that end at a node adjacent to the start node. However, for a 6 by 6 grid, there are 458,696 Hamiltonian paths but only 1,072 Hamiltonian cycles. (Sloane A096969 and A003763)

The analysis in  R. Stoyan and V. Strehl: Enumeration of Hamiltonian Circuits in Rectangular Grids. Journal of Combinatorial Mathematics and Combin.Computing 21 (1996), 197-127, identifies an alternative way of identifying Hamiltonian cycles. For example, this figure shows a Hamiltonian Cycle for a 6 by 6 grid.

Stoyan and Strehl point out that each cell is either inside or outside the Hamiltonian Cycle, as shown here (yellow cells inside, white outside) Thus, Hamiltonian Cycles for an N by N graph can be associated with an "induced subgraph" of an (N-1) by (N-1) square graph.

Stoyan and Strehl show that any induced subgraph corresponds to a Hamiltonian Cycle if: A) It is a tree B) No 2 by 2 sub-grid of the extended grid matches one of the four patterns:

  Additionally, there are always $\frac{N^2-2}{2}$ inside cells and $\frac{(N-2)^2}{2}$ outside cells, and the four corner cells have to be inside.

These constrants can be used to find subgraphs that correspond to Hamiltonian cycles more efficiently than the search of Hamiltonian paths. For N=6, there are $\binom{(N-1)^2-4}{\frac{(N-2)^2}{2}} = \binom{21}{8} = 203,490$ combinations of outside cells that need to be tested.

However, the algorithm does not scale well. For N=8, there are $\binom{45}{18} =  1,715,884,494,940$ combinations of outside cells.

The performance could be improved by using the observation that there cannot be 2 contiguous outside cells on the boundary. However the algorithm as it stands runs in less than 1 second for N=6, and the suggested improvement would not significantly reduce the number of cases that would need to be tested for N=8.

Python Implementation

A Python implementation of an algorithm based on these constraints is presented below. The search for the four patterns of 2 by 2 sub-cells does not cover the extended grid, as it turns out that this is not necessary, at least for the cases N=4 and N=6 (I haven't worked out whether this extends to higher values of N)

Dent, Aye Gill Pike

I camped at High Laning campsite in Dent on a very pleasant sunny evening, and next day walked a circuit from Dent along the ridge of Aye Gill Pike.

View from High Laning campsite

 

   

Although the ridge isn't marked on OS maps as a footpath, it is on access land. There are footpath signs throughout its length and stiles over all walls and fences.

Click for an interactive map

Gate on Dales Way

Mire House

Stopping at the village shop in Dent to buy some pasties for lunch, I walked down to the river Dee, following the Dales Way heading West through numerous fields and gates to Ellers, where I took the footbridge across the river and followed the path up through Mire House, Craggs Farm and Hewthwaite, picking up the Dales Way again.




Before reaching Millthrop, there are good views of Sedbergh, in front of the Howgills.

Sedbergh and the Howgills

Turning East just before Millthrop, I followed a footpath that became increasingly indistinct, taking a bearing East across Frostrow to pick up a bridleway on the far side. This section was quite boggy and hard going. A shorter alternative route (shown in green on the map), would avoid this "off path" section.

Aye Gill Pike

From the end of the bridleway, it is a simple matter of following the wall up to the summit of Aye Gill Pike.

Cowgill Church

From the summit, I followed the wall East to Snaizwold Fell, then followed a ruined wall down to a track which runs past Cowgill Church, and to the Dales Way at Ewegales.






I then  followed the Dales Way all the way back to Dent.

That will teach them!

River Dee

 

Enjoying a well-earned retirement from  show business

Burtersett, Semer Water, Askrigg

A brief spell of decent weather, so I went up to the Dales to walk from Burtersett across to Semer Water and Askrigg.

Click the map image for an interactive map

Parking at the top of Burtersett village, where there is ample parking space, I set off following the bridleway to Wether Fell.

Crossing the Roman Road, I followed the footpath initially signposted to Marsett, taking a turning towards Countersett and Semer Water after a few hundred yards.

A brief detour into Countersett Village, and then on to Semer Water for lunch.

 

Semer Water feeding into river Bain

Semer Water

      

River Bain

After lunch, I followed the river Bain to Bainbridge, and doubled back just before Bainbridge to climb up to Scar Top, to avoid walking along the main road. 

There is a dilemma of where to drop down from Scar Top back to the Ure river - the shorter route to Askrigg is across a set of stepping stones, but the stones are likely to be underwater in moderately high water conditions. The longer option is to drop down to Worton village (blue route on map) where there is a bridge over the river Ure. From the bridge, there is a flagstone path through the fields to Askrigg.



A brief stop at the Kings Arms in Askrigg (once used as the Drovers in the TV series All Creatures Great and Small), and then following Skelgill Lane and down to Shaw Cote to cross the Ure at a set of stepping stones near Catriggs Farm,  that are always above water level.




Then across the main road and up Mitre Bank Lane to Burtersett. Altogether a very pleasant circuit.

Testing whether a number is a perfect square

Introduction

A simple way to test whether a whole number is a perfect square is to take its square root, square the integer part and compare the result to the original number. In Python this might be coded as follows (the +0.5 is to avoid rounding errors)

from math import sqrt
def issquare(n):
  return int(sqrt(n) + 0.5) ** 2 == n

However, a preliminary test can avoid the need to calculate the square root for some numbers. Perfect squares always end in 0,1,4,5,6 or 9, so numbers ending in  2,3,7 or 8 could immediately be eliminated by looking at the remainder after dividing by 10.

Similarly, a perfect square divided by 16 always leaves a remainder of 0,1,4 or 9. Numbers with remainders 2,3,5,6,7,8,10,11,12,13,14,15 (75% of numbers) can be eliminated. As 16 is a power of 2, $16=2^4$, the remainder can be obtained in two ways: by division or by finding the last 4 bits by masking. In Python these could be implemented as:

Obtaining remainder by division from math import sqrt SR16= frozenset((0, 1, 4, 9)) def issquare(n): if n%16 in SR16 : return int(sqrt(n) + 0.5) ** 2 == n return False

Obtaining remainder by masking from math import sqrt SR16= frozenset((0, 1, 4, 9)) def issquare(n): if n & 15 in SR16 : return int(sqrt(n) + 0.5) ** 2 == n return False

Which divisor produces the most efficient pre-test?

Defining $s(n)$ to be the number of possible residues of square numbers modulo n, a formula for $s(n)$ is derived by Stangl, W. D. "Counting Squares in ℤn, Math. Mag. 69, 285-289, 1996. The formula is summarised in Wolfram Mathworld - Square Number. 

Defining                                                       $r(n) = $ $\frac{s(n)}{n}$, 

we are interested in numbers with small values of $r(n)$. In the examples above, s(10)=6, r(10)=0.6,  s(16)=4, r(16)=0.25.

Stangl shows that $s(n)$ is multiplicative, i.e $s(ab)=s(a)s(b)$ if $a$ and $b$ are co-prime, so $r(n)$ is also multiplicative, and is therefore defined by its values for $p^n$ where $p$ is prime. The following graph shows the value of $r(p^n)$ for primes up to 29

Values of $r(2^n)$ look much more promising than powers of other primes, but Stangl's formula shows that $r(2^n)$ tends towards $\frac{1}{6}$ as n increases, so there are diminishing returns in choosing larger values of $2^n$ as a pre-test divisor.

Can other composite divisors produce smaller values of $r(n)$?

The above graph shows that for primes greater than 2, there is no benefit in including a factor of $p$ higher than $p^2$ in $n$ to reduce $r(n)$. A few powers of 2 may have a benefit in reducing $r(n)$.

This graph shows $r(n)$ for all values of n below 10,000. We are interested in the values of n at the lower edge of the graph, highlighted with a blue line. These are values of $n$ for which $r(n) < r(m)$ for all $m < n$
Defining the set   $Opt=\{n: r(n) < r(m)$ for all $m < n \}$ this graph shows $r(n)$ values of $n$ in $Opt$ up to 100,000 Values of $r(n)$ below the general trend for $n$ in $Opt$ are highlighted. Their prime factorisation shows the trend of the numbers: 16 = 24 144 = 24.32 720 = 24.32.5 5,040 = 24.32.5.7 55,440 = 24.32.5.7.11
Extending this trend, this graph shows values of r(n) for the following values of n: 16 = 24 144 = 24.32 720 = 24.32.5 5,040 = 24.32.5.7 55,440 = 24.32.5.7.11 720,720 =  24.32.5.7.11.13 12,252,240 =  24.32.5.7.11.13.17 232,792,560 =  24.32.5.7.11.13.17.19 5,354,228,880 =  24.32.5.7.11.13.17.19.23

$r(n)$ reaches a tantalisingly small 0.16%, but for n=5,354,228,880 (larger than 2³²), and for $s(n)=$8,709,120. 

Testing different divisors

The following graph tests the divisors listed above and divisors of the form $2^n$, by calculating the time to test all numbers in the range 1 to 10,000,000. For divisors of the form $2^n$ , two forms of Python function are tested, using division and masking to obtain the remainder.

For comparison, the time taken by the simplest issquare function is shown in yellow

The graph shows that the performance improves for divisors of the form $2^m$ up to $2^7$, and then levels out. The graph also shows that there is no significant advantage in using masking to calculate a number modulo $2^m$ (blue points) compared to straightforward division (green points).

The performance of the best composites (red points) is noticably better than the performance of  powers of 2 of similar magnitude. The best performance is for D= 55,440 = 2⁴.3².5.7.11, after which the performance degrades.

Pre calculating the residues of squares modulo D

The overhead of pre-calculating the residues of square numbers modulo D needs to considered when choosing the pre-test divisor.

Using the following algorithm, the table shows the time taken to generate the set of residues of squares modulo n. The table shows that the set of square residues mod 55,440 can be calculated in 2ms

SR={0} D=1 for b in [2**4,3**2,5,7,11]: squares_mod_b = set([(x*x)%b for x in range(b)]) SR = set([ r + n*D for r in SR for n in range(b) if (r+n*D)%b in squares_mod_b ]) D*=b

Factor introduced  D  r(D) s(D) Time to generate residues of squares  (ms) 16   16 25.00%  4  0.01 9 144 11.11%  16  0.12 5 720 6.67%  48  0.23 7  5,040 3.81%  192  0.53 11   55,440 2.08%  1,152  2.01

We can now define algorithms with the best pre-test. Two options are presented, one with a hard coded set of square residues, and one with a calculated set.

$s(720)=48$, which is a reasonable number of square residues to hard-code into an algorithm. An implementation of issquare using D=720 is:

from math import sqrt
SR = frozenset([0,1,4,385,324,649,256,144,145,121,580,409,576,25,640,265,\
                  544,289,180,676,369,169,304,49,436,9,441,36,64,160,196,481,\
                  585,484,81,340,625,601,225,100,16,529,361,496,241,400,244,505])
def issquare(n):
  if n%720 in SR : 
    return int(sqrt(n) + 0.5) ** 2 == n
  return False

An implementation using D=55,440, with the square residues being constructed dynamically:

from math import sqrt

SR={0}
D=1
for b in [2**4,3**2,5,7,11]:
  squares_mod_b = set([(x*x)%b for x in range(b)])
  SR =  set([ r + n*D for r in SR for n in range(b)
              if (r+n*D)%b in squares_mod_b ])
  D*=b


def issquare(n):
  if n%D in SR: 
    return int(sqrt(n) + 0.5) ** 2 == n
  return False

For a further increase in speed of approximately 33%, at the expense of readability, function calls could be replaced with in-line code, for example:

Function calls count=0 for n in xrange(10000000): if issquare(n): count+=1

In-line code count=0 for n in xrange(10000000): if n%D in SR and int(sqrt(n) + 0.5) ** 2 == n: count+=1

Enigma 1736, or solving $x^3=x$ mod $10^N$

The problem posed by New Scientist Enigma 1736 was to find the largest 4 digit number with all digits different whose cube has the same last 4 digits as the original number.

Generalising the problem to finding an N digit number whose cube has the same last N digits as the original number, i.e. solutions of $x^3=x$ mod $10^N$, (without the constraint of all digits being different) we can rewrite the equation as

$x^3-x = (x-1)x(x+1)=0$ mod $10^N$

For $N$ $\geq$ $3$ there are always fifteen solutions, one for each of the cells in the table. Five (in grey) have an immediate solution, the other ten can be found by solving three linear diophantine equations (red, green and blue).

		$5^N | (x-1)$	$5^N |x $	$5^N | (x+1)$
$2^N | (x-1) $	$2|(x+1)$	$1$	$(r$ mod $2^N)5^N$ $r5^N+s2^N=1$	$2(r$ mod $2^{N-1})5^N-1$ $r5^N+s2^{N-1}=1$
$2^N| x $		$10^N-(r$ mod $2^N)5^N+1$ $r5^N+s2^N=1$	$0$	$(r$ mod $2^N)5^N-1$ $r5^N+s2^N=1$
$2^N| (x+1)$	$2 | (x-1)$	$10^N-2(r$ mod $2^{N-1})5^N+1$ $r5^N+s2^{N-1}=1$	$10^N-(r$ mod $2^N)5^N$ $r5^N+s2^N=1$	$10^N-1$
$2^{N-1}| (x-1)$	$ 2 | (x+1)$	$5^N 2^{N-1}+1$	$(r$ mod $2^{N-1})5^N$ $r5^N+s2^{N-1}=1$	$2(r$ mod $2^{N-2})5^N-1$ $r5^N+s2^{N-2}=1$
$2^{N-1}| (x+1)$	$2 | (x-1)$	$10^N-2(r$ mod $2^{N-2})5^N+1$ $r5^N+s2^{N-2}=1$	$10^N-(r$ mod $2^{N-1})5^N$ $r5^N+s2^{N-1}=1$	$5^N 2^{N-1}-1$

Complementary pairs of solutions, $x$ and $10^N-x$ occur on opposite sides, as illustrated by the example for N=4

		625 | (x−1)	625 | x	625 | (x+1)
16 | (x−1)		1	625	1249
16 | x		9376	0	624
16 | (x+1)		8751	9375	9999
8 | (x−1)		5001	5625	6249
8 | (x+1)		3751	4375	4999

Here is a Python implementation to find solutions:

Another slip of the tongue

A cracker from a continuity announcer this afternoon:

"At 2:15, Patrick Malahide stars as Albert Speer, or prisoner number five as he was known throughout his twenty years in Spandau Ballet"

I think Speer played the saxaphone.

Enigma 49

New Scientist magazine's Enigma #49 problem can be solved with a bit of number theory. Generalising the problem to finding a number whose square has the same last N digits as itself:

z² = z mod 10^N  →  z(z-1) = 0 mod 10^N. One factor of z(z-1) is odd, the other even. The even factor is a multiple of 2^N.

For a solution other than 0 or 1, the odd factor of z(z-1) must be a multiple of 5^N (if the even factor is a multiple of 5 it is a multiple of 10, so the odd factor is congruent to 1 or 9 mod 10 and therefore not a multiple of 5, so the even factor is a multiple of 10^N).

So the solution is one of
a)  z=2^Nx,    z-1=5^Ny
b) z-1=2^Nx,   z=5^Ny

Solutions to the Diophantine equation 2^Nx+ 5^Ny=1  produce the solutions
a) z=2^N(x mod 5^N)
b) z=5^N(y mod 2^N)

So, some Python code. Function egcd is a standard recursive implementation of the Extended Euclidean Algorithm to find solutions to a linear Diophantine equation (and the gcd as a by-product).

def egcd(a,b):
  if b == 0:
    return [1,0,a]
  else:
    x,y,g = egcd(b, a%b)
    return [y, x - (a//b)*y, g] 

for N in range(1,40):
  x,y,g = egcd(5**N, 2**N)
  print "N =",N, sorted([(x%2**N)*5**N, (y%5**N)*2**N])

A slip of the tongue

This had me laughing for several minutes.

"Squawk"

Matt Ridley talking on "The Value of Culture" on Radio 4 this morning (about 6 mins 30 sec in from the start):

"I live in a culture called science which is a tribe, but that tribe has no particular place in the world, but yet it is just as narrow as if it were a particular New Guinea group of people who killed birds of paradise with blowtorches"