Factoring numbers in Python and C++

While trying to solve the "Squares on a Cube" puzzle on Contest Center, I became sidetracked into writing an efficient program to produce the prime factors of a number, an exercise that most programmers will have attempted at some time.

The hybrid Python / C++ code presented here combines well known techniques, Miller Rabin and Brent's variation of Pollard Rho, together with a modern fast technique for modular reduction developed by Rutten and Eekelen.

Python implementation

After a bit of experimenting, I settled on this mixture for a Python implementation:

• Lookup tables for numbers below 10⁶
• Trial division of primes below 300
• Miller-Rabin primality test (deterministic up to the published limit)
• Brent's variant of the Pollard Rho algorithm, by default running for up to 1 second
• Elliptic Curve Method (ECM) if the Brent algorithm fails to find a factor within its time limit. 

C++ implementation

While the Python version is reasonably fast, a C++ version  is much faster. My C++ code factors numbers below 2⁶⁴, where Brent Pollard Rho can be used without having to use ECM or Multiple Polynomial Quadratic Sieve.

The performance of Brent Pollard Rho and Miller Rabin is ultimately dominated by modular multiplication, so any improvement of modular multiplication time is reflected in the overall performance of the factorisation algorithm. Here are my attempts to speed up modular multiplication:

I. Shift and add

To calculate $a \times b$ mod $m$  I initially used an intricate, and relatively slow, shift and add method. Several implementations of this can be found on the internet. The version I used was stolen from Craig McQueen's post on stackexchange.  This version is valid for any $ m < 2^{64} $

Function modmulSA implements this technique.

II, Repeated reduction of most significant 64 bits

  My first attempt to speed up modular multiplication, valid for a modulus $m < 2^{63}$,  uses the following techniques:

a) Division by multiplication

If a modulus of the same denominator needs to be obtained many times, as in the Brent algorithm and the Miller Rabin test, an efficient  technique is to construct an inverse $M=2^k/m$ of the denominator $m$ once (M is often termed a "magic number"), then perform division by $m$ by multiplying the numerator by M and bit shifting to divide by $2^k$.  Of course it's a bit more complicated than that, and is described comprehensively by Henry S. Warren Jr in Hackers Delight, (Chapter 10, Integer Division by Constants), and explained in a readable form by Ridiculous Fish in Labor of Division (Episode I).

C++ functions magicu2 and magicdiv (stolen from Hackers Delight) and magicmod implement these techniques.

b) Modular multiplication

1. Reduce a and b modulo m (using the division by multiplication technique)
2. Construct the product $c = a \times b$. If $a$ and $b$ are 64 bit numbers, $c$ is a 128 bit number. I used the MS VC++ intrinsic function for this calculation, but if this is not available, Hackers Delight function mulul64 can be used.
3. Repeatedly find the most significant 64 bits of $c$ and reduce them modulo $m$ (again using division by multiplication), until c is reduced to a number less than $m$

Function modmulRR implements this technique.

III, Assembler

On 64 bit Intel processors, the multiply instruction multiplies two 64 bit numbers and stores the 128 bit result in two registers, rdx:rax. The divide instruction divides a 128 bit number stored in rdx:rax by a 64 bit number and stores the 64 bit quotient in rax and the 64 bit remainder in rdx.

So these instruction are ideal for modular multiplication. However, the intrinsic function to perform division of a 128 bit number is not available in MS Visual Studio, so a few lines of assembler (mod64.asm) have to be written.

The assembler version has the advantage of being valid for a modulus up to $2^{64}-1$, and is noticeably faster than repeated reduction, and of course much faster than the shift and add method.

Function modmulAS is the C interface to this function.

IV. Rutten-Eekelen

An even faster method of modular multiplication than assembler, for a modulus $m<2^{63}$, uses the algorithm described in Efficient and formally proven reduction of large integers by small moduli by Luc M. W. J. Rutten and Marko C. J. D. van Eekelen. This method requires the pre-calculation of a similar, but slightly different, magic number to the one described above, and then makes use of this number in an intricate algorithm whose correctness has been verified using a computer generated proof.

Function modmulRE implements this function.

Performance

This graph shows the average time to factor numbers in the range $10^n$ to $10^n+10000$ (giving a representative mix of easy and hard factorisations) for all my C++ versions, and for reference, a Python implementation of Brent Pollard and Miller Rabin. The graph shows that the shift and add version has performance no better than the Python version, and that the Rutten-Eekelen version beats the Assembler version, for numbers below $2^{63}$

C++ / Python integration

The ctypes module integrates Python with a DLL of the C++ implementation. Calling a DLL from Python  incurs an overhead of about 1.5µs, so it is faster to use the Python implementation for small numbers that are factored using a lookup table. For larger numbers, the overhead soon becomes negligible compared to the time to factorise the number.

Rutten-Eekelen has the best performance for a modulus $m<2^{63}$, even beating the assembler version. For a modulus $2^{63} \le m \lt 2^{64}$ the assembler version is fastest, so the final C++ version called from Python uses a hybrid of these two methods.

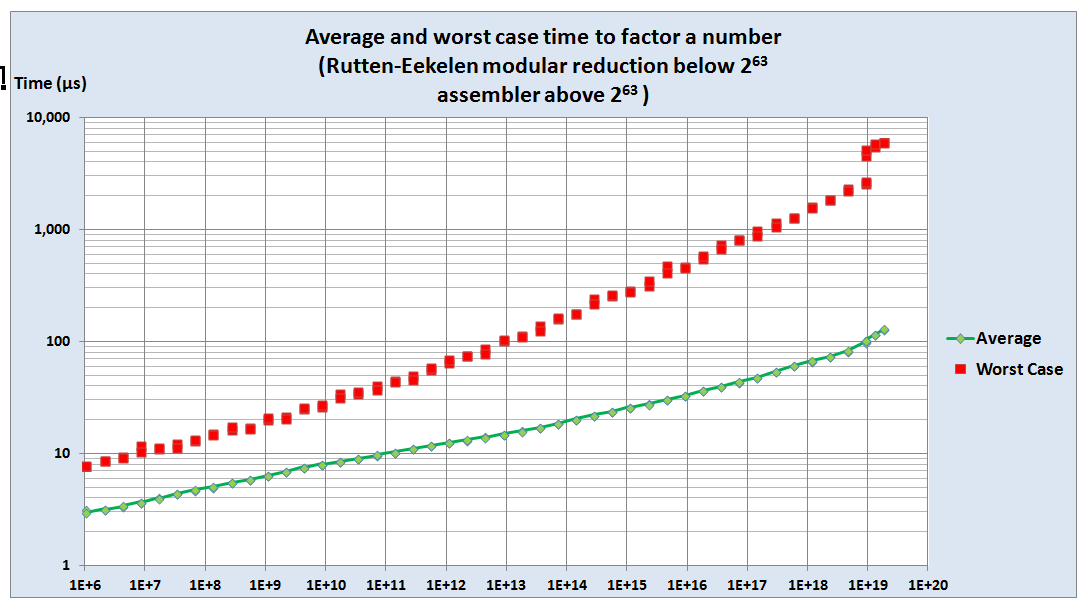
To verify that the Brent Pollard Rho algorithm copes with difficult cases, this graph shows the average and worst case times to factorise numbers within $ \pm 5000$ of various baselines. Note the jump in worst case factorisation times for numbers $ \ge 2^{63}$, where the algorithm switches from Rutten-Eekelen to Assembler.

The worst cases are listed here.

Source Code 

All the source code is located here, except for the optional ECM algorithm, for which I used the Sourceforge implementation pyecm.py.

A stand-alone Python module, factors.py can be run without the C++ DLL or the ECM module being present. 
This module has the following principal functions:

Description	Example call	Return value
all_factors(n) returns a list of all the factors of n The function chooses whether to use the Python or C++ version depending on the size of n.	all_factors(12)	[1,2,3,4,6,12]
totient(n) returns the Euler totient function	totient(30)	8
factorise(n, maxBrentTime=1.0) returns a list of the prime factors of n maxBrentTime determines how many seconds the Brent algorithm should run before reverting to ECM  (if available). The function chooses whether to use the Python or C++ version depending on the size of n.	factorise(12)	[2,2,3]

 
A DLL, FactorsDLL.dll,  built on Windows 7 64 bit, is included, together with a Python module factorsDLL.py to call the DLL from Python. I'm not sure whether the DLL will work on other machines. In case it doesn't, the source code to build the DLL is also included.

 Implementation notes

The Miller Rabin test can occasionally derive a factor of a composite number, when testing witness $a$ for the primality of $n$ encouters the situation

$a^{2^rd} \ne \pm 1$ mod $n$  and  $a^{2^{r+1}d} =1$ mod $n$

In this situation  $gcd(a^{2^rd}-1,n)$ produces a factor of $n$. I have included this test, even though the condition rarely occurs in practice.

The Brent Pollard Rho algorithm occasionally fails to find a factor of a composite, so I simply run the algorithm again. The random selection of parameters seems to ensure that the algorithm does not have to be run too many times to obtain a factor.

Postscript

Even though the program vastly reduced the time to factorise a number, I still haven't solved the Contest Center problem that motivated me to write it.