The problem statement is:
The five cities of Genoland are interconnected by four national highways A, B, C and D. They are also independently linked by four provincial highways 1, 2, 3 and 4. Each highway connects two cities and Geno is the only city which can be directly reached from every other city. A round trip of the five cities involves the five highways 1, 3, 4, B and C or 1, 2, A, C and D or 2, 3, A, B and C (not necessarily in the order given).
Which of the highways reach Geno?
No pair of cities is connected by both a national and provincial highway (this can be deduced from the round trips). There are two possible configurations that have eight highways connecting five cities:
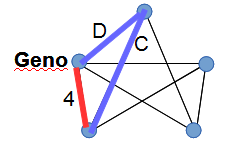
Configuration A does not provide three round trips, so the five cities are connected in configuration B. We can immediately deduce which city is Geno:
The three round trips are:
Highway C appears in all three round trips, so we can deduce which highway is C. Highways D and 4 appear in only one round trip each, so we can also deduce 4 and D (national highways are blue, provincial are red)
Highway 1 is in the same round trips as highways 4 and D, so we can deduce highway 1:
As all cities are connected via provincial highways, the remaining highway from the top city must be a provincial. Similarly, as all cities are connected via national highways the remaining highway connecting the bottom right city must be a national:
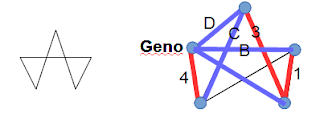
The round trip using highway 4 uses highways 1,3,4,B,C, so we can deduce which highways are B and 3 :
Similarly, the round trip using highway D uses highways 1,2,A,C,D so we can deduce which highways are A and 2 :
So Geno is reached by highways A,B,D,4






No comments:
Post a Comment